矩形同士の当たり判定
意外と簡単なのだが、焦ると間違える。
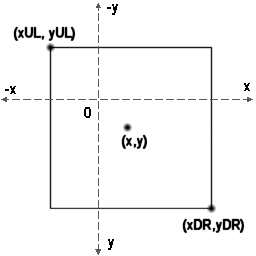
まず、ここで扱う矩形とは、2次元上の平面において、下図の様にオフセットとなる点(x,y)があり、
そこから相対的に最小最大の点(xUL, yUL), (xDR, yDR)を取った範囲の事。
この説明では領域の境界面も含めてあたり判定を考えてみる。
2つの矩形が接触しているか判定するためには、単純に2つの領域で論理積を取り、一部でも重なる場合は真となるため、接触しているとみなす。(下図参照)
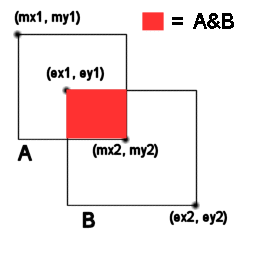
ここで演算を簡略化するために、
(mx1, my1) = (mx+mxUL, my+myUL)
(mx2, my2) = (mx+mxDR, my+myDR)
(ex1, ey1) = (ex+exUL, ey+eyUL)
(ex2, ey2) = (ex+exDR, ey+eyDR)
と置くことにする。また、式中の記号は次の意味を表す。
&& -> 論理積(AND)
|| -> 論理和(OR)
! -> 否定(NOT)
まず、判定式は単純にX座標から見ていくと、
mx1
<=
ex2 && ex1
<=
mx2
となり、下図の塗りつぶされている所が上記式の範囲。
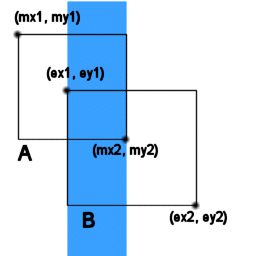
同様にY座標の判定式も、
my1
<=
ey2 && ey1
<=
my2
となる。よって、下図の様に、X座標の場合と、Y座標の場合の論理積が一部でも存在すれば、当たりとみなせる。
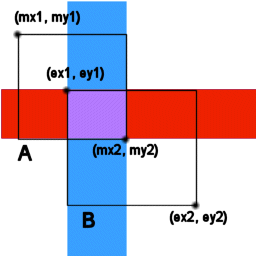
まとめ
2つの矩形が接触しているか判断するためには、以下の式を評価して、結果が真になれば接触してると判断できる。
(mx1
<=
ex2 && ex1
<=
mx2
&&
my1
<=
ey2 && ey1
<=
my2)
Sample(適当)
※補足
ド・モルガンの法則ってのが存在して、そいつを適用すると、判定式は次のように書くこともできる。
!
(mx1
<=
ex2 || ex1
<=
mx2
||
my1
<=
ey2 || ey1
<=
my2)
Back
2005/7/22 Gyabo



